The World of Real Numbers

This will begin with a description of real numbers, completeness, compactness, and some topology—ultimately leading to integration and differentiation.

Real Numbers

These are the numbers you and I know: 0, 1, -1, 1.5, and even $\pi$. Rational numbers are ones we can represent as an integer divided by another. It turns out many numbers are irrational including $\pi$, $\sqrt{2}$, $\sqrt{3}$, and $\sqrt{n}$ for any $n$ that's not a perfect square ($\neq$ a number squared).

Idea: use divisibility to show no rational number squared is 2.

1. if $\sqrt{2} = a / b$, then $2 = a^2 / b^2$ $\implies a^2$ is divisible by 2

2. So $a$ must be divisible by 2, implying $b^2$ is also divisible by 2, a contradiction!

More abstractly, the real numbers are uniquely determined by a handful of natural requirements on a set:

• field (operations: +, x with identity, inverses, commutiativity, associativity, and distribution)

• order: trichotomy (either >, < or =)

• completeness (= least upper bound property)

  • every set with an upper bound has a least upper bound.

    • e.g., (0, 1) has 1 as an upper bound, but 1 is not in the set (0, 1)

A nice consequence of this is the triangle inequality: $\| x + y \| \leq \|x\| + \|y\|$ for any $x, y \in \mathbb{R}$.

Idea: look at cases where x, y are positive (Spivak has a nice proof of this)

It turns out even in $\mathbb{R}^n$, a nice property about order called Cauchy Schwarz holds:

$$|\vec{u} \cdot \vec{v} | \leq |\vec{u}| | \vec{v} |$$

why? The idea is to use $\vec{u} \cdot \vec{v} = |u||v| \cos($ angel between them$)$.

primary::Vector

a vector is a point in $\mathbb{R}^n$

• it looks like $(x_1, x_2, x_3)$ where each $x$ is in $\mathbb{R}$

dot product is an operation on two vectors defined as:

$(x_1, x_2, x_3) \cdot (y_1, y_2, y_3) = x_1y_1 + x_2y_2 + x_3y_3$

Finally, how many real numbers are there? Cantor showed there are actually uncountably many---you can never come up with a way to write a list of all real numbers even if you had all the time in the world.

Idea: suppose someone claimed to have a list of all reals (this list would have to be infinite). Then, we write down a number that's different from each one on the list in the nth decimal place

Nevertheless, the set of rationals is countable. Make a table:

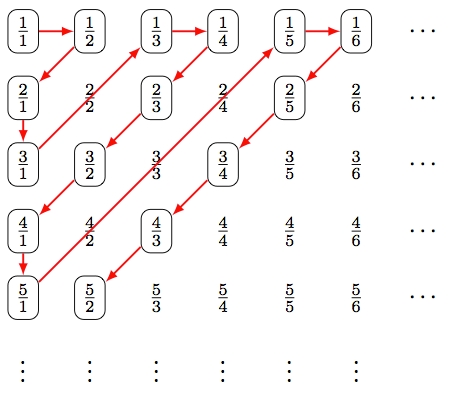
This is a great TedEd video discussing infinity and the reals.

warning::Infinity + or -

is not in the set of real numbers

Fundamental Theorem of Arithemetic: every integer can be factor into primes

Set Theory

A set of ordered pairs if called a relation.

A one-to-one (or injective) function sends inputs to distinct outputs

f(a) = f(b) implies a = b

A onto (or surjective) function hits all outputs with some input.

DeMorgan's Law: $(A \cap B)^c = A^c \cup B^c$

idea: draw a picture (venn diagram) to see it's true.

Topology

Distance

We can define a more general way to measure distance between two points in $\mathbb{R}^n$ (or any vector space), called a norm, denoted || * ||.

A norm is (for $x, y \in \mathbb{R}^n$):

1. positive (||x|| > 0, for all x in the set); definite || x || = 0 if and only if x =0

2. ||ax|| = a||x||, for any a in $\mathbb{C}$
3. triangle: $\| x + y \| \leq \| x \| + \| y \|$

Common examples are Euclidean distance (L2 norm), Taxi Cab (L1 norm), and sup-norm (returns the peak value across all dimesions of vector; sup is the least upper bound, which isn't always in the set of interest).

remember vectors spaces are sets with nice properties about addition and scalar multiplication

Norms in this context will later generalize to classes of functions with nice integration properties in measure theory.

primary::L2 and Lp norms

$(\sum_i |x_i|^p )^{1/p}$

In the case of L2, p = 2 (this will show up again in measure theory).

More generally we can talk about metric spaces, rather than just $\mathbb{R}^n$ or a vector space with a norm. A metric space is any set M with a distinace metric, d: MxM -> [0, ∞) such that

1. symmetric: _d(a, b) = d(b, a) for a, b in M

2. definite: d(a, b) = 0 if and only if a = b

3. triangle: _d(a, c) ≤ d(a, b) + d(b, c)

Many of the topological properites we'll explore applies to general metric spaces: all you need is a set and a reasonable way to measure distance.

info::topological space

is a set M and a collection of subsets, S, that contains the empty set & M, is closed under union, and finite intersections.

e.g., the open sets of a metric space always form a topological space!

Neighborhoods

With a notion of distance (often, we use L2 or Euclidean distance), we can define neighborhoods or open balls around a point:

B(x; r) is a ball of radius r around x = set of points which are within a distance r of x (strictly < here)

formally, $B(a; r) = \{ x \in set : \|\| x - a \|\| < r \}$

A set is open, if for any point, there is an open ball (of any radius) entirely contained in the set.

It turns out even open set is the union of open balls (potentially infinitely many). Why?

1. for each x in the Open set, there is a radius r such that B(x, r) ≤ Open set

2. the union of all these B(x, r) (for each x in the open set) covers the open set

3. but each B(x, r) is contained in the open set ==> U B(x,r) = Open set!

A set is closed, if the set's complement is open.

warning::closed and open

are not mutually exclusive; a set can be both! (for example $\mathbb{R}$ and $\emptyset$ )

An accumulation (or limit point) of a set is one where every open ball centered at the limit point contains at least one other point in the set. Alternatively, we can think of a limit point as the limit of some sequence of points in the set.

This leads to another characterization of closed sets: sets that contain all their limit points.

Unions and Intersections of Open and Closed Sets

U Open is Open	Intersection of Closed is Closed
For any x in U open, x is contained in some open set. So there is B(x, r) entirely contained in some open set, hence contained in the U open sets.	similar lidea to open sets

in pictures, I think of the union of a bunch of open intervals, which is going to be open. For closed, I think about the intersection of a bunch of closed intervals [0, 1], [1\/4, 3\/4], ... this will be closed, because worst case, it'll contain a single point. While, not rigorous, this helps me imagine what's going on.

Compactness

A metric space is compact if every open cover has a finite subcover. An open cover is a union of open sets containing the metric space.

It turns out there's a relationship between compactness and sequences in a space. If every sequence in space has a convergent subsequence, we say the the space is sequentially compact. It turns out sequentially compact and compact are equivalent in any metric space!

warning:: In Topological Spaces

sequentially compact and compact are not equivalent

A compact metric space is always complete, meaning every Cauchy sequence converges.

idea: Given any Cauchy sequence, a_n, we can always find a convergent subequence (by sequential compactness). Since the sequence is Cauchy, the terms must be arbitrarily close to the convergent subsequence, hence converge.

Cantor's Intersection Theorem

In a compact space X, if closed, nonempty sets C1, C2, ... are nested: C1 $\supseteq$ C2 $\supseteq$ C3 ... then

$$\cap C_n \neq \emptyset$$

Idea: suppose $\cap C\_n = \emptyset$, then 1. Let $O\_n = X \setminus C\_n$ for each n 2. Then U On is an open cover for X => there is a finite subcover 1. say $\cap\_{n=1}^k O\_n$ 3. Yet, because C_n are nested, only a single O_i covers X 4. Then $C\_i = X \setminus O\_i = \emptyset$, a contradiction!

This will be used to show two famous theorems: Bolzano-Weierstrass and Heine-Borel.

warning:: the set of reals

is not compact

Bolzano-Weierstrass Theorem

Every bounded sequence in $\mathbb{R}^n$ has a convergent subsequence.

bounded means contained in a ball of finite radius

Why is this true? We'll chop our bounds in half and use the nested intervals theorem:

Heine-Borel

A set K in $\mathbb{R}$ is compact <====> it's closed and bounded

primary::Tool

a closed subset, C, of a compact, K, set is compact

1. Let U O be an open cover of C

2. U O U {K C} is open and covers K

3. there is a finite subcover of K, hence one for C

With this tool we can now show why Heine-Borel is true

idea:

1. => Bounded: suppose not

   1. there exists some unbounded sequence, an

   2. every subsequence is also unbounded, contradicting Bolzano-Weierstrass

2. => closed: idea show K already contains its boundary

   1. choose x in K's closure

   2. there is a sequence xn in K converging to x

   3. xn is Cauchy, implying xn must converge to a point in K

      1. hence x is in K

3. <= Compact: 1. K is inside some interval [-M, M], because it's bounded 2. Since K is closed and [-M, M] is compact, K is closed 1. by our Tool above!

[notes transcribed]

Big Picture

What have we accomplished? We showed x, y, and z...

TODO:

• understand abstraction level between various spaces (metric, vector, function) and their corresponding distance measures.